本記事はアフィリエイト広告(PR)を含みます
今回はニューラルネットワークの出力層でよく使われる「ソフトマックス関数」を実装してみる。
1. ソフトマックス関数
ソフトマックス関数は以下の式で表される。
\[y_k=\frac{e^{a_k}}{\sum_{i=1}^{n}e^{a_i}}\]
この式は出力n個に対してk番目の出力\(y_k\)を求めています。
ソフトマックス関数はすべての出力の合計が1になるように変換され、各出力を確率としてとらえることができるので分類問題などによく用いられます。
スポンサーリンク
2. ソフトマックス関数の実装
Eigenを使ってソフトマックス関数を実装します。
ソースコードは以下の通り。
// Softmax関数
void softmax(MatrixXf& mat_in, MatrixXf& mat_out) {
int i;
MatrixXf mat_e;
MatrixXf mat_e_sum;
MatrixXf mat_e_sum_calc = MatrixXf::Zero(mat_in.rows(), mat_in.cols());
// 入力データのexp計算
mat_e = mat_in.array().exp();
// 入力データexpの行ごとの合計を計算
mat_e_sum = mat_e.rowwise().sum();
// サイズを合わせるためmat_exp_sumをコピー
for (i = 0; i < mat_in.cols(); i++) {
mat_e_sum_calc.col(i) = mat_e_sum.col(0);
}
// 出力計算
mat_out = mat_e.array() / mat_e_sum_calc.array();
}実際に関数の動作を確認してみます。
ソースコードはこちら。今回は0.3, 2.9, 4.0を入力し、出力を計算します。
#include < iostream >
#include "Eigen\\Core"
using namespace std;
using namespace Eigen;
// Softmax関数
void softmax(MatrixXf& mat_in, MatrixXf& mat_out) {
int i;
MatrixXf mat_e;
MatrixXf mat_e_sum;
MatrixXf mat_e_sum_calc = MatrixXf::Zero(mat_in.rows(), mat_in.cols());
// 入力データのexp計算
mat_e = mat_in.array().exp();
// 入力データexpの行ごとの合計を計算
mat_e_sum = mat_e.rowwise().sum();
// サイズを合わせるためmat_exp_sumをコピー
for (i = 0; i < mat_in.cols(); i++) {
mat_e_sum_calc.col(i) = mat_e_sum.col(0);
}
// 計算確認用
cout << "e:" << mat_e << endl;
cout << "e_sum:" << mat_e_sum << endl;
cout << "e_sum_calc:" << mat_e_sum_calc << endl;
// 出力計算
mat_out = mat_e.array() / mat_e_sum_calc.array();
}
int main() {
MatrixXf mat_input = MatrixXf::Zero(1, 3);
MatrixXf mat_output = MatrixXf::Zero(1, 3);
mat_input(0, 0) = 0.3;
mat_input(0, 1) = 2.9;
mat_input(0, 2) = 4.0;
softmax(mat_input, mat_output);
cout << "入力:" << mat_input << endl;
cout << "出力:" << mat_output << endl;
return 0;
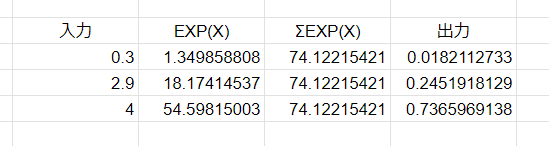
}出力はこのようになりました。
e:1.34986 18.1741 54.5981
e_sum:74.1222
e_sum_calc:74.1222 74.1222 74.1222
入力:0.3 2.9 4
出力:0.0182113 0.245192 0.736597表計算で計算した結果と比較すると正常に動作していることが分かりますね。
3. オーバーフロー対策
指数関数の値が大きくなってしまった場合にオーバーフローを起こすことがあるのでその対策をします。よく用いられるのは各入力値から入力値の最大値を引く方法です。
// Softmax関数(オーバーフロー対策)
void softmax_maxdiff(MatrixXf& mat_in, MatrixXf& mat_out) {
int i;
MatrixXf mat_e;
MatrixXf mat_in_max;
MatrixXf mat_e_sum;
MatrixXf mat_in_max_calc = MatrixXf::Zero(mat_in.rows(), mat_in.cols());
MatrixXf mat_e_sum_calc = MatrixXf::Zero(mat_in.rows(), mat_in.cols());
// 入力値の最大値を算出
mat_in_max = mat_in.rowwise().maxCoeff();
for (i = 0; i < mat_in.cols(); i++) {
mat_in_max_calc.col(i) = mat_in_max.col(0);
}
mat_e = (mat_in.array() - mat_in_max_calc.array()).exp();
mat_e_sum = mat_e.rowwise().sum();
for (i = 0; i < mat_in.cols(); i++) {
mat_e_sum_calc.col(i) = mat_e_sum.col(0);
}
mat_out = mat_e.array() / mat_e_sum_calc.array();
}最初に実装した関数とオーバーフロー対策を行った関数で動作を確認して比較してみます。ソースコードはこちら。今回は1010, 1000, 990を入力して確認してみます。
#include < iostream >
#include "Eigen\\Core"
using namespace std;
using namespace Eigen;
// Softmax関数
void softmax(MatrixXf& mat_in, MatrixXf& mat_out) {
int i;
MatrixXf mat_e;
MatrixXf mat_e_sum;
MatrixXf mat_e_sum_calc = MatrixXf::Zero(mat_in.rows(), mat_in.cols());
// 入力データのexp計算
mat_e = mat_in.array().exp();
// 入力データexpの行ごとの合計を計算
mat_e_sum = mat_e.rowwise().sum();
// サイズを合わせるためmat_exp_sumをコピー
for (i = 0; i < mat_in.cols(); i++) {
mat_e_sum_calc.col(i) = mat_e_sum.col(0);
}
// 計算確認用
cout << "e:" << mat_e << endl;
cout << "e_sum:" << mat_e_sum << endl;
cout << "e_sum_calc:" << mat_e_sum_calc << endl;
// 出力計算
mat_out = mat_e.array() / mat_e_sum_calc.array();
}
// Softmax関数(オーバーフロー対策)
void softmax_maxdiff(MatrixXf& mat_in, MatrixXf& mat_out) {
int i;
MatrixXf mat_e;
MatrixXf mat_in_max;
MatrixXf mat_e_sum;
MatrixXf mat_in_max_calc = MatrixXf::Zero(mat_in.rows(), mat_in.cols());
MatrixXf mat_e_sum_calc = MatrixXf::Zero(mat_in.rows(), mat_in.cols());
// 入力値の最大値を算出
mat_in_max = mat_in.rowwise().maxCoeff();
for (i = 0; i < mat_in.cols(); i++) {
mat_in_max_calc.col(i) = mat_in_max.col(0);
}
mat_e = (mat_in.array() - mat_in_max_calc.array()).exp();
mat_e_sum = mat_e.rowwise().sum();
for (i = 0; i < mat_in.cols(); i++) {
mat_e_sum_calc.col(i) = mat_e_sum.col(0);
}
// 計算確認用
cout << "in_max:" << mat_in_max_calc << endl;
cout << "e[maxdiff]:" << mat_e << endl;
cout << "e_sum[maxdiff]:" << mat_e_sum << endl;
cout << "e_sum_calc[maxdiff]:" << mat_e_sum_calc << endl;
mat_out = mat_e.array() / mat_e_sum_calc.array();
}
int main() {
MatrixXf mat_input = MatrixXf::Zero(1, 3);
MatrixXf mat_output = MatrixXf::Zero(1, 3);
MatrixXf mat_output_maxdiff = MatrixXf::Zero(1, 3);
int count = 0;
mat_input(0, 0) = 1010;
mat_input(0, 1) = 1000;
mat_input(0, 2) = 990;
softmax(mat_input, mat_output);
softmax_maxdiff(mat_input, mat_output_maxdiff);
cout << "入力:" << mat_input << endl;
cout << "出力:" << mat_output << endl;
cout << "出力(オーバーフロー対策):" << mat_output_maxdiff << endl;
return 0;
}出力結果はこのようになりました。
通常の関数では値が-nan(ind)になってしまいますが、対策を行った関数では結果が出力されました。
e:inf inf inf
e_sum:inf
e_sum_calc:inf inf inf
in_max:1010 1010 1010
e[maxdiff]:1 4.53999e-05 2.06115e-09
e_sum[maxdiff]:1.00005
e_sum_calc[maxdiff]:1.00005 1.00005 1.00005
入力:1010 1000 990
出力:-nan(ind) -nan(ind) -nan(ind)
出力(オーバーフロー対策): 0.999955 4.53979e-05 2.06106e-09表計算の結果はこちら。正常に計算できてそうです。
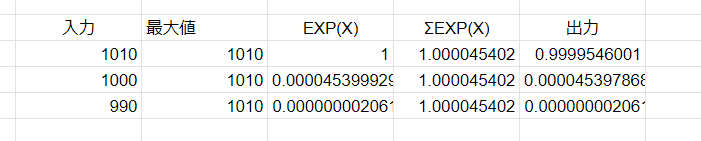
今回は以上です。
4. 参考書籍
リンク
スポンサーリンク




コメント